正四棱柱的定义(棱柱与基本几何体的组合)
首先,我们知道,由正多边形构成的棱锥有三种,即等棱长的正三棱锥、正四棱锥、正五棱锥。它们的底面分别是正三角形、正方形、正五边形,而侧面都是正三角形。
其次,根据棱锥接在棱柱上面的位置的不同,有三种可能情况:第一种,接在棱柱的顶面(或底面);第二种,接在棱柱的侧面;第三种,同时接在顶面(或底面)和侧面。下面我们分类讨论。
(一)接在顶面(或底面)
此时用来组合的棱柱有三种:正三棱柱、正四棱柱和正五棱柱。如果是相接的是棱锥的侧面,只需考虑两种情况:正三棱柱的顶面接正四棱锥,或正五棱锥(把正三棱锥的各个面都看成底面,暂不考虑)。用磁力片不难发现,得到的均是凹多面体。
也就是说,与棱柱相接的总是棱锥的底面。此时,如果只在棱柱上接一个棱锥,便得到正三棱锥柱、正四棱锥柱、正五棱锥柱;如果上下各接一个,便得到双三棱锥柱、双四棱锥柱、双五棱锥柱。
(二)接在侧面
等棱长的棱柱,侧面都是正方形,因此,能接的棱锥只能是正四棱锥。计算可知,正四棱锥的侧面与底面的夹角约为54.74°,因此棱柱的顶面的每个内角不能超过180°-54.74°=125.26°。
我们知道,正六边形的一个内角为120°,正七边形的一个内角为128.57°,也就是说与棱锥相接的棱柱最多为正六棱柱。
另外,对于正三棱柱而言,可以在两个相邻侧面各接上一个棱锥,因为60°+2×54.74°<180°;而对于正四棱柱则不行,因为90°+2×54.74°>180°;而正五棱柱及以上,显然更不行。
这样,我们便得到了所有棱锥接在棱柱侧面的9个结果,示意图如下:
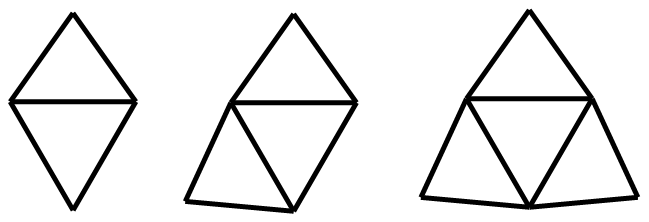
① 侧锥三棱柱、二侧锥三棱柱、三侧锥三棱柱;
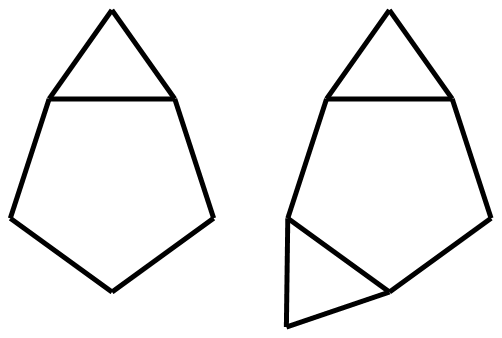
② 侧锥五棱柱、二侧锥五棱柱;
③ 侧锥六棱柱、双侧锥六棱柱、二侧锥六棱柱、三侧锥六棱柱

其中没有正四棱柱,是因为正四棱柱就是正方体,其侧面与顶面是一样的,所有可能的结构就是情况(一)中的正四角锥柱和双四角锥柱。
(三)同时接在顶面(或底面)和侧面
因为顶面和底面的位置是相同的,我们不妨先假设顶面和侧面都有。顶面可以接正三棱锥、正四棱锥或正五棱锥,可以算得这三种棱锥的侧面与底面的夹角分别约为70.53°、54.74°和37.38°,而侧面只能接正四棱锥。如果用垂直于顶面和侧面的平面去截这个多面体,其截面会有一个内角至少为37.38°+90°+54.74°=182.12°>180°。而凸多面体要求任何一个平面去截它,截面都是凸多边形。
因此,这种情况是不能构成约翰逊多面体的。
至此,所有棱柱与棱锥相组合的情况都清晰了,一共15种,把它们罗列如下:

正三棱锥柱
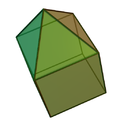
正四棱锥柱
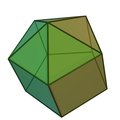
正五棱锥柱
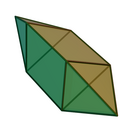
双三棱锥柱

双四棱锥柱
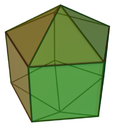
双五棱锥柱
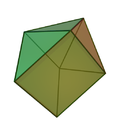
侧锥三棱柱

二侧锥三棱柱

三侧锥三棱柱
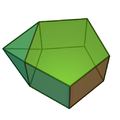
侧锥五棱柱
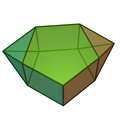
二侧锥五棱柱
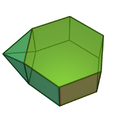
侧锥六棱柱
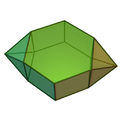
双侧锥六棱柱
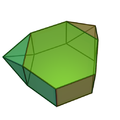
二侧锥六棱柱
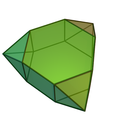
三侧锥六棱柱





